Using variations of VAEs (Part 2)

See Part 1

Drawbacks of traditional VAE

A couple weeks ago, I went to a computer vision workshop and discussed my research with other students at JHU. There, I got the idea to try some other forms of VAEs to promote “disentangled representations.” On a high level, this means learning a latent space where each latent dimension controls some different aspect of the resulting image.

Furthermore, I learned that VAEs suffer from so-called “posterior collapse”¹. It seems that there’s a lot written about this, but it seems I completely missed it when I was starting off this project. The idea behind this is that if the decoder is sufficiently powerful, then it doesn’t matter what sort of latent representation we learn. Instead, the model encodes the information into the decoder’s parameters. This is really bad for our application, since the whole point is to use the VAE to learn a useful latent factors.

After the conference, I had a couple new directions – I put my latent space manipulation experiments on hold. The first task was to make sure I wasn’t suffering from posterior collapse, and the second task was to try variations of VAEs that enforce disentangled representations.

VAEs

Traditional VAE

I started off with using a traditional VAE, where the encoder and decoder networks were 2-layer CNNs and I experimented with different latent dimensions $z$ as my main hyperparameters. Results were alright, in the sense that reconstructions were good. In the following example, the top row is the original image and the bottom row is the reconstruction.

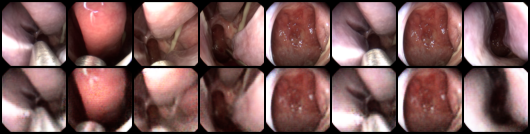
However, doing interpolation between image encodings in latent space didn’t seem to preserve tools at all points in the interpolation, and it was hard to make sense of the latent dimensions. It turns out that this was because it was learning an entangled representation.

From these experiments, at least I validated that even a somewhat weak VAE could learn a good reconstruction of the surgical images. Furthermore, I learned from StackExchange that we expect KL-divergence to decrease quickly at first and only increase later.

$\beta$-VAE

I first learned of $\beta$-VAE through Lilian Weng’s blog post. The $\beta$-VAE paper can be found here.

To talk about $\beta$-VAEs, it’s important to review traditional VAE². VAEs are based on variational inference, where our objective is to maximize the the evidence lower bound (ELBO)

$\mathcal{L}(p_\theta,q_\phi) = \mathbb{E}_{q_\phi(z|x)} \left[ \log p_\theta(x,z) - \log q_\phi(z|x) \right]$

over the space of $q_\phi$. The ELBO satisfies the equation

$\log p_\theta(x) = KL(q_\phi(z|x) || p(z|x)) + \mathcal{L}(p_\theta,q_\phi).$

We can also reformulate the ELBO as

$\log p(x) \geq \mathbb{E}_{q_\phi(z|x)} \left[ \log p_\theta(x|z) \right] - KL(q_\phi(z|x) || p(z))$

In the context of images, this has a nice intuitive explanation – we are summing the KL-divergence and the pixel-wise reconstruction loss. We can think of the KL-divergence as acting as a regularizer on the reconstruction loss.

The idea behind $\beta$-VAE is simple – we’re just increasing the regularization. We do this by multiplying the KL-divergence by a weight parameter $\beta$. Thus our objective function becomes

$\log p(x) \geq \mathbb{E}_{q_\phi(z|x)} \left[ \log p_\theta(x|z) \right] - \beta KL(q_\phi(z|x) || p(z))$

When $\beta=1$ we have a standard VAE. But, when $\beta>1$ we encourage more disentangled representations. To understand why this is the case, I think it’s best to let the original authors do the explaining: https://arxiv.org/pdf/1804.03599.pdf

InfoVAE

e.g. MMD-VAE https://ermongroup.github.io/blog/a-tutorial-on-mmd-variational-autoencoders/

---

1. Slide 5 of http://www.people.fas.harvard.edu/~yoonkim/data/sa-vae-slides.pdf ↩

2. Equations from https://ermongroup.github.io/cs228-notes/extras/vae/ ↩